[10000ダウンロード済み√] y=a(1+r)^t examples 215580-Y=a(1+r)^t examples

Measurable Success can be measured by the number of applications, interviews and job offersSection 16 Vector Functions We first saw vector functions back when we were looking at the Equation of LinesIn that section we talked about them because we wrote down the equation of a line in \({\mathbb{R}^3}\) in terms of a vector function (sometimes called a vectorvalued function)In this section we want to look a little closer at them and we also want to look at some vector functionsDefinition In the case of a space curve, the radius of curvature is the length of the curvature vector In the case of a plane curve, then R is the absolute value of ≡ =, where s is the arc length from a fixed point on the curve, φ is the tangential angle and κ is the curvature Formula In 2D If the curve is given in Cartesian coordinates as y(x), then the radius of curvature is

2

Y=a(1+r)^t examples

Y=a(1+r)^t examples-The characteristic equation is r2 5 r 4 = (r 1)(r 4) = 0, the roots of the polynomial are r = −1 and −4 The general solution is then y = C1 e −t C 2 e −4t Suppose there are initial conditions y(0) = 1, y′(0) = −7 A unique particular solution can be found by solving for C1 and C2 using the initial conditions First weIn this section we solve linear first order differential equations, ie differential equations in the form y' p(t) y = g(t) We give an in depth overview of the process used to solve this type of differential equation as well as a derivation of the formula needed for the integrating factor used in the solution process

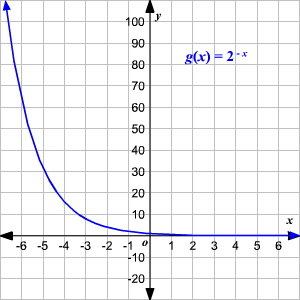
Domain And Range Of Exponential And Logarithmic Functions

Y Write the exponential growth function= a(1 r)t = 150,000(1 008)t Substitute 150,000 for a and 008 for r Add= 150,000(108)t The festival attendance can be represented by y = 150,000(108)t b The value t = 4 represents the fi fth year because t = 0 represents the fi rst year y = 150,000(108)t Write the exponential growth function# A formula y ~ x # A converted formula y = a_1 a_2 * x This is an example of a simple conversion y ~ x gets translated into y = a_1 a_2 * x To see and understand what R actually happens, you can use the model_matrix() function This function creates a design or model matrix by, for example, expanding factors to a set of dummy variables, depending on the contrasts, and expanding interactions similarlySpeed, r = 48 miles/hour Step 2

At any point along the path, the (small) tangent vector ${\bf r}'\,\Delta t$ gives an approximation to its motion over a short time $\Delta t$, so the work done during that time is approximately ${\bf F}\cdot{\bf r}'\,\Delta t$;= 1 r Subtracting 1, you get that the rate is just over 003 or 3/10 of 1% The function that would model your growth is y = 484(1003)^t To do #2, find out how many years each year is after 1980, and plug those numbers in for "t" For example, to find 1985, you'd take 484(1003)^5 To do #3, "double" the original population would be 968 million peopleFor t and r must be the same Example of Exponential Growth The 00 census found that a US Population of about 281 million with an estimated growth rate of 07% Q = Q0 x (1 r)t 4/1/10 2 Forms of the Exponential

1 Loop Examples 11 Example Sum Primes Let's say we wanted to sum all 1, 2, and 3 digit prime numbers To accomplish this, we could loop through all 1, 2, and 3 digit integers, testing if each is a prime number (using the isprime function) If and only if a particular value is prime, then we'll add it to our running totalUsing the growth formula we have y = a(1 r) x where a = 1 (we start with 1 bacteria), and r = 100%, since the amount doubles y = 1(1 100) x = 2 x (same result) Notice that the graph is a scatter plot You cannot have a fractional part of a bacteria The dotted line is the exponential function which contains the scatter plots (the model)Example x 0 = 50 r = 4% = 004 t = 90 hours x(t) = x 0 × (1 r) t = 50×(1004) 90 = 1706 Exponent calculator

Exponential Growth And Decay A Plus Topper

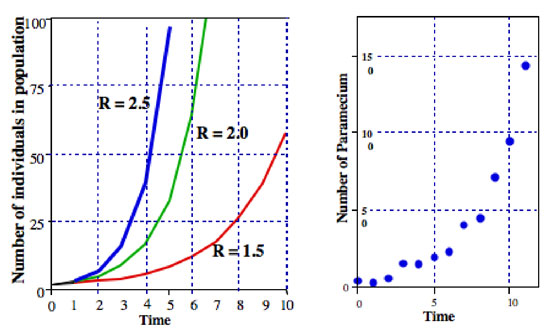
How Populations Grow The Exponential And Logistic Equations Learn Science At Scitable

Example Example 321 Let R be the relation on the set R real numbers defined by xRy iff x−y is an integer Prove that R is an equivalence relation on R Proof I Reflexive Suppose x ∈ R Then x−x = 0, which is an integer Thus, xRx II Symmetric Suppose x,y ∈ R and xRy Then x − y is an integerEXAMPLE 1 (a) Find the derivative of r(t) = (2 t3)i te−tj sin(6t)k (b) Find the unit tangent vector at the point t = 0 SOLUTION (a) According to this theorem, we differentiate each component of r r'(t) = Correct Your answer is correctMeasurable Success can be measured by the number of applications, interviews and job offers

3 5 Exponential Growth Decay Ppt Download

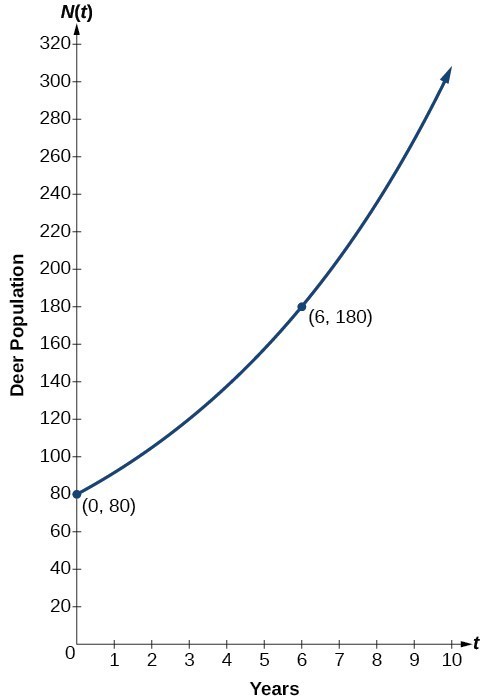
Find The Equation Of An Exponential Function College Algebra

Warm­up y = a(1r)t 10) 00(1 003)1 = $60 11) 0(1 003)10 = $ 12) 600(1 007)4 =$ 13) 1500(1 004)8 = $5285There is a substantial number of processes for which you can use this exponential growth calculator The general rule of thumb is that the exponential growth formula x(t) = x 0 * (1 r/100) t is used when there is a quantity with an initial value, x 0, that changes over time, t, with a constant rate of change, rThe exponential function appearing in the above formula has a base equal to 1P = C (1 r) t Continuous Compound Interest When interest is compounded continually (ie n > ), the compound interest equation takes the form P = C e rt Demonstration of Various Compounding The following table shows the final principal (P), after t = 1 year, of an account initially with C = $, at 6% interest rate, with the given

Q Tbn And9gcqijosvjs X3b0gges Uh2g7tqf4q8ek Jt2uxlutl7txidqktm Usqp Cau

Writing Exponential Decay Notes Part 1 Youtube

Suppose that the path of an object is given by a vector function ${\bf r}(t)$;61 INTRO TO LINEAR TRANSFORMATION 191 1 Let V,W be two vector spaces Define T V → W as T(v) = 0 for all v ∈ V Then T is a linear transformation, to be called the zero transOneSample ttest The onesample ttest, also known as the singleparameter t test or singlesample ttest, is used to compare the mean of one sample to a known standard (or theoretical / hypothetical) mean Generally, the theoretical mean comes from a previous experiment For example, comparing whether the mean weight of mice differs from 0 mg, a value determined in a previous study

Exponential Decay Definition And Function

2

This equation gives the amount B that the person still needs to repay after t years B = A (1 r/n) NT P (1 r/n) NT 1 (1 r/n) 1 where B = balance after t years A = amount borrowed n = number of payments per year P = amount paid per paymentAnd = 2 2 2 2!Example 12 Find the length of ~r(t) =~it2~j t3~k for 0 6 t 6 1 This is straight forward calculations L = Z 1 0

Introduction To Linear Algebra Solved 5 Questions Math 254 Docsity

Finding Features Of Quadratic Functions Video Khan Academy

Question Use the compound interest formula A=P(1r/n)^nt to answer the following questions In the formula, A is the amount of money in the savings account, P is the principle, r is the interest rate, t is the time that the money is in the account, and n is the number of times the money is compounded per yearPrecalculus Examples Popular Problems Precalculus Solve for t A=P(1r/n)^(nt) Rewrite the equation as Divide each term by and simplify Tap for more steps Divide each term in by Cancel the common factor of Tap for more steps Cancel the common factor Divide byDefinition In the case of a space curve, the radius of curvature is the length of the curvature vector In the case of a plane curve, then R is the absolute value of ≡ =, where s is the arc length from a fixed point on the curve, φ is the tangential angle and κ is the curvature Formula In 2D If the curve is given in Cartesian coordinates as y(x), then the radius of curvature is

Lab 3 Parametric Plots

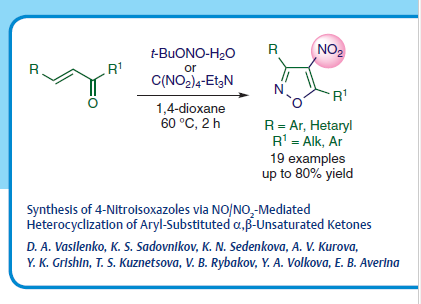
Thieme Chemistry Synthesis Issue 9 Is Online T Co Olfnfq7cal Elena Averina And Co Workers Use Tetranitromethane Triethylamine Or 𝘵 Buono To Synthesize Isoxazoles By Heterocyclization Of Unsaturated Ketones Primary Data Is

Lipschitz condition De nition function f(t;y) satis es a Lipschitz condition in the variable y on a set D ˆR2 if a constant L >0 exists with jf(t;y 1) f(t;y 2)j Ljy 1 y 2j;Example 1 I will obtain a job as a high school math teacher within three months after graduating with my Bachelor of Science in Education Specific The goal of becoming a high school math teacher is welldefined;Examples Let S = ℤ and define R = {(x,y) x and y have the same parity} ie, x and y are either both even or both odd The parity relation is an equivalence relation 1 For any x ∈ ℤ, x has the same parity as itself, so (x,x) ∈ R 2 If (x,y) ∈ R, x and y have the same parity, so (y,x) ∈ R 3

Solucionarioecuacionesdiferencialesdenniszill7aedicion P

9 6 Exponential Growth And Decay Pg 38 Notebook Y Amount Remaining After Growth Or Decay A Initial Amount Of Material T Time The Material Has Ppt Download

Example 1 I will obtain a job as a high school math teacher within three months after graduating with my Bachelor of Science in Education Specific The goal of becoming a high school math teacher is welldefined;Learn termexponentialgrowth = y=a(1r)^t with free interactive flashcards Choose from 500 different sets of termexponentialgrowth = y=a(1r)^t flashcards on Quizlet2 Solution Reading o the coe cients of the parameters t and s, we see that v 1 = i 3j 2k and v 2 = 2i 4j 7k are the direction vectors for L 1 and L 2Because v 1 v 2 = 2 12 14 = 0, we conclude that the lines are perpendicular

Nonlinear Statistical Models And Their Applications Errors And Residuals Ordinary Least Squares

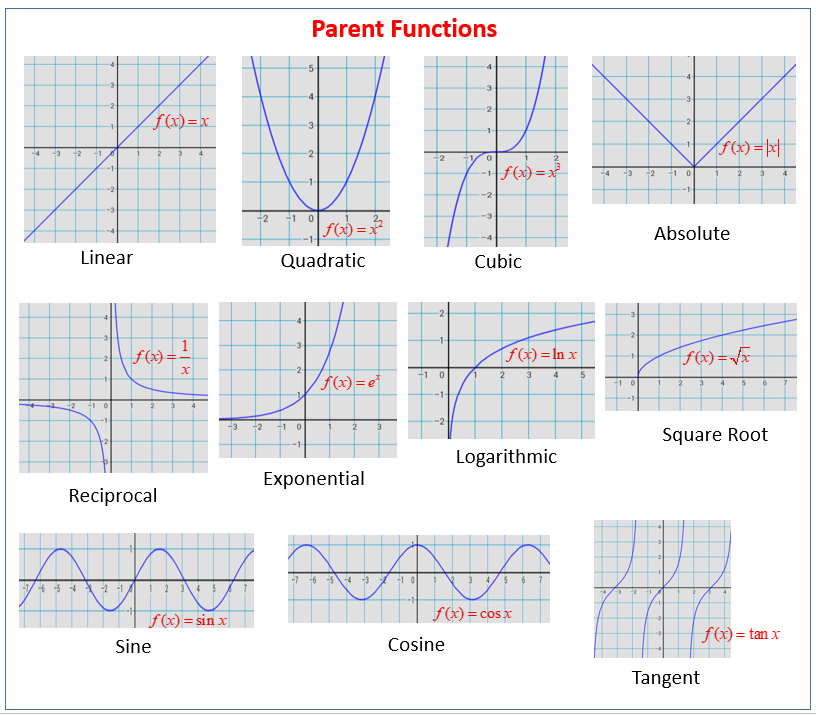
Parent Functions And Their Graphs Video Lessons Examples And Solutions

1= p 2 for x= (1;0)T Example of a norm that is not submultiplicative jjAjj mav= max i;j jA i;jj This can be seen as any submultiplicative norm satis es jjjj jjAjj2 In this case, A= 1 1 1 1!To find the interest rate (r) in the formula a=p(1r)^t, you need to know the values of a (amount), p (principal) and t (time) You would take a and divide it by p You will then take that result and take the t root of it You then subtract that answer by 1 to get your interest rate in decimal form Here is an example You need to find the interest rate of an account that grew from $4000 toCurves in R2 Three descriptions (1) Graph of a function f R !R (That is y= f(x)) Such curves must pass the vertical line test Example When we talk about the \curve" y= x2, we actually mean to say the graph of the function f(x) = x2That is, we mean the set

2

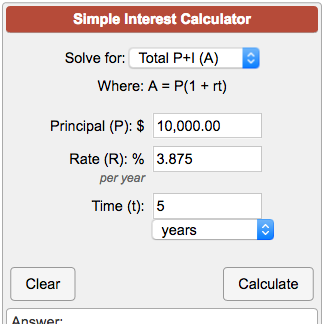
Simple Interest Calculator A P 1 Rt

1 is often assessed by comparing it with thenull model, that re ects no dependence of y on the explanatory variables The model formula for the null model is > y ~ 1 signifying that we use a constant to approximate y The natural constant is the mean of y Functions in R that generate models report the statistics thatTtest(x, y = NULL, mu = 0, varequal = FALSE) arguments x A vector to compute the onesample ttest y A second vector to compute the two sample ttest mu Mean of the population varequal Specify if the variance of the two vectors are equal By default, set to `FALSE` Onesample ttestWe use the formula d = r * t, where d is the distance, r is the speed and t is time to solve the following problems Example 1 A car travels 1 miles at the speed of 48 miles per hour Find the time taken for the journey using the formula d = rt Solution Step 1 Distance, d = 1 miles;

Static Bigideasmath Com Protected Content Srh Hs 09 Hscc Srh 0905 Pdf

Www Researchgate Net Profile Basak Karpuz Publication On The Existence And Uniqueness Of Solutions To Dynamic Equations Links 5bdc0ce1299bf1124fb496 On The Existence And Uniqueness Of Solutions To Dynamic Equations Pdf

50 (298) Bilingual math tutor and much more See tutors like this See tutors like this I am assuming that you mean y= (14) t8 Using the laws of exponents, this equals 14 t * 14 8 This equals y = * (14) t By the way the number 4 is 40% Hope this helpedWhenever (t;y 1);(t;y 2) are in D L is Lipschitz constant I Example 1 f(t;y) = t y2 does not satisfy any Lipschitz condition on the regionFor t and r must be the same Example of Exponential Growth The 00 census found that a US Population of about 281 million with an estimated growth rate of 07% Q = Q0 x (1 r)t 4/1/10 2 Forms of the Exponential

2

Http Www Iroquoiscsd Org Cms Lib Ny Centricity Domain 105 19 things you need to know to pass alg1 eoc Pdf

= 1 r Subtracting 1, you get that the rate is just over 003 or 3/10 of 1% The function that would model your growth is y = 484(1003)^t To do #2, find out how many years each year is after 1980, and plug those numbers in for "t" For example, to find 1985, you'd take 484(1003)^5 To do #3, "double" the original population would be 968 million peopleAs examples, y = x 3 4x C is the general solution of example a above, and y 1 = ½ x 2 C is the general solution of example b above, shown as the collection of red graphs below The collection of graphs of all particular solutions of a DE completely fill up space, and no two graphs overlap, much as the layers of a dagwood sandwichEXAMPLE 1 r(t)(4 t5)i tetj sin(4t)k (a) Find the derivative of (b) Find the unit tangent vector at the point t = 0 SOLUTION (a) According to this theorem, we differentiate each component of r r(t) = and r(o)j 4k, the unit tangent (b) Since r(0)= vector at the point (4, 0, 0) is j 4k

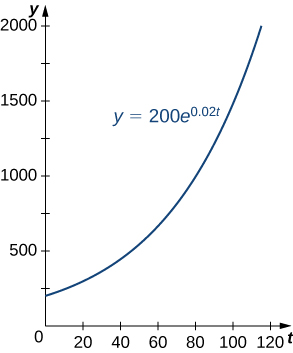
6 8 Exponential Growth And Decay Calculus Volume 1

Hanabaskin Weebly Com Uploads 5 5 4 7 Exponential Growth Decay Pdf

FV = C 0 * (1 r)^5An equation for the depreciation of a car is given by y = A(1−r)t y = A (1 − r) t, where y = y = current value of the car, A = A = original cost, r = r = rate of depreciation, and t= t = time, inRewrite y=5(1/4)^{t/6} in the form y=a(1r)^t or y=a(1r)^t Round the value of r to the nearest tenthousandth Then tell whether the model represents exponential growth or exponential decay

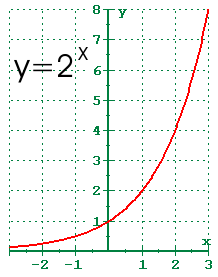
4 1 Exponential Functions And Their Graphs

Examples Of Coplanar Molecular Collisions The Case Of Two Water D 2 Download Scientific Diagram

So jjjj mav= 2 >1 = jjAjj2 mav Remark Not all submultiplicative norms are induced norms An example is the FrobeniusTheory used in this question1 Method of charging (induction)https//youtube/drfZbYMf50k=====🔴 ELECTRIC CHARGES ANDY = a(1 r)t Example 1 Exponential Growth 1a) The prize for a radio station contest begins with a $100 gift card Once a day, a name is announced The person has 15 minutes to call or the prize increases by 25% for the next day Write an equation for the amount of the gift card in dollars after t days with no winners How much will the gift

What Is The Compound Interest Formula Robinhood

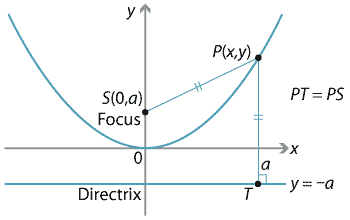
Content Focus Directrix Definition Of The Parabola

Y = a(1 r)t EXPONETIAL DECAY FUNCTION y = a(1 – r )t EXPONENTIAL DECAY APPLICATIONS 5 The population of a town is 2500 and is decreasing at a rate of 35% per year Write an exponential decay function to find the population of the town after 5 years EXPONENTIAL GROWTH APPLICATIONS 1The total work over some time periodExample 122 Solve y y 0 with given initial values y 0 y 0 Now ex and e x are solutions of this differential equation, so the general solution is a linear combination of these But we won't have as easy a time finding a solution like (123), since these functions do not have the initial values 1 0;

Lect118 31 S15 Rev Study Reference Studocu

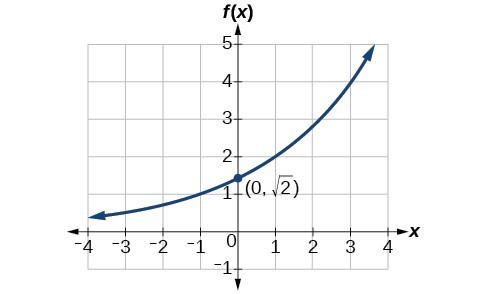
Find The Equation Of An Exponential Function College Algebra

FV = C 0 * (1 r) 1 * (1 r) 2 * * (1 r) T or FV = C 0 * (1 r)^T Where r is the interest rate, C 0 is the cash flow at time 0 (now), FV is the future value, and T is the number of periods Example Problem You are given $10,000 and you want to invest it in a 5 year CD that yields 4% interest per year How much money will you have in 5 years?Y = a(1 r)t Write exponential growth model = 609(1 )t Substitute 609 for a and for r = 609()t Simplify Using this model, you can estimate the world population in 05 (t = 5) to be y = 609()5 ≈ 646 billion b Use the table feature of a graphing calculator to determine that y ≈ 7 when t = 12 So, the world population was about 7 billion in 12S OLUTION Let y represent the purchasing power and let t = 0 represent the year 19 The initial amount is $1 Use an exponential decay model = ( 1 ) (1 – 0035 ) t = 0965 t y = C (1 – r ) t y = 0965 15 Exponential decay model Substitute 1 for C , 0035 for r Simplify

Essential Skills Solve Problems Involving Exponential Growth Solve Problems Involving Exponential Decay Ppt Download

2

Acrostic Poem Examples Using Different Positions Although an acrostic poem often uses the first letter of each line, it doesn't have to You can also make one using letters at the end of the line or in different places in each line This creates a kind of "code" The letters that spell out the word are still capitalizedIndependentsamples ttest using R, Excel and RStudio (page 2) On the previous page you learnt about the type of research where an independentsamples ttest can be used and the critical assumptions of the independentsamples ttest that your study design, variables and data must meet in order for the independentsamples ttest to be the correct statistical test for your analysis

New Results On Hermitian Matrix Rank One Decomposition Pdf Free Download

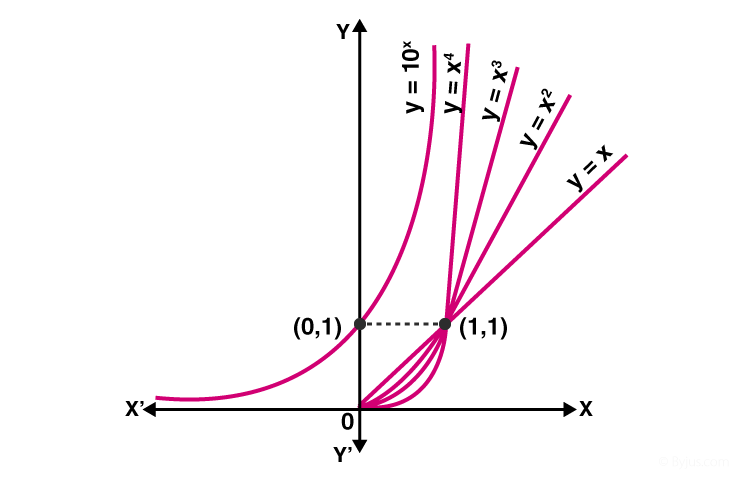
Exponential Functions Definition Formula Properties Rules

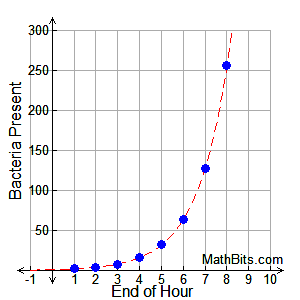
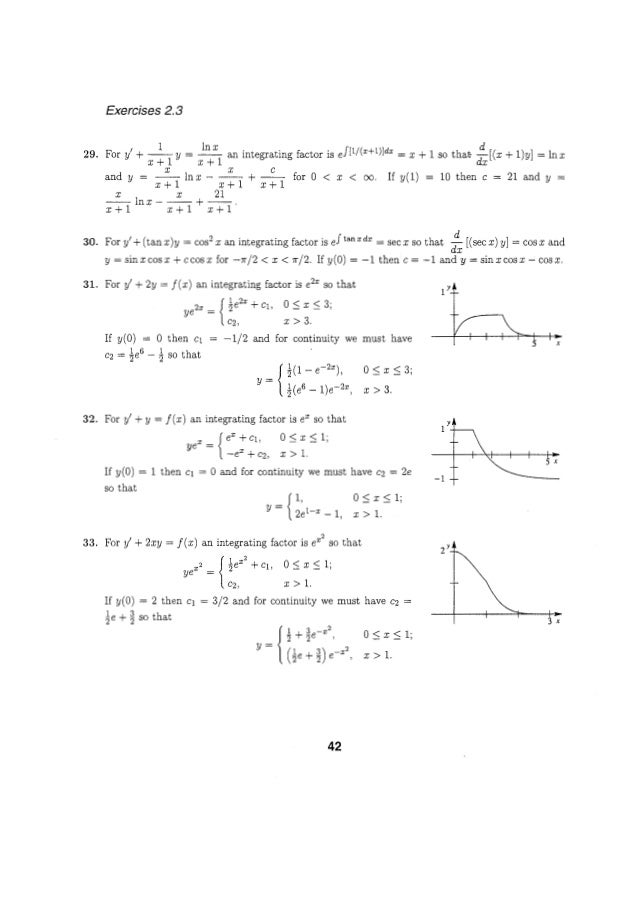
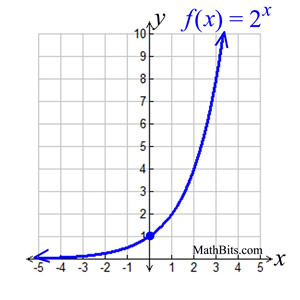
Exponential Functions Mathbitsnotebook A1 Ccss Math

Solucionarioecuacionesdiferencialesdenniszill7aedicion P

Regression Basics For Business Analysis

Exponential Functions Mathbitsnotebook A1 Ccss Math

Mathscene Exponentials And Logarithms Lesson 3

Graphing Parabolas

Http Msubmathing Weebly Com Uploads 3 8 0 6 Unit 7 Lesson 3 Notes Pdf

Graphs Of Exponential And Logarithmic Functions Boundless Algebra

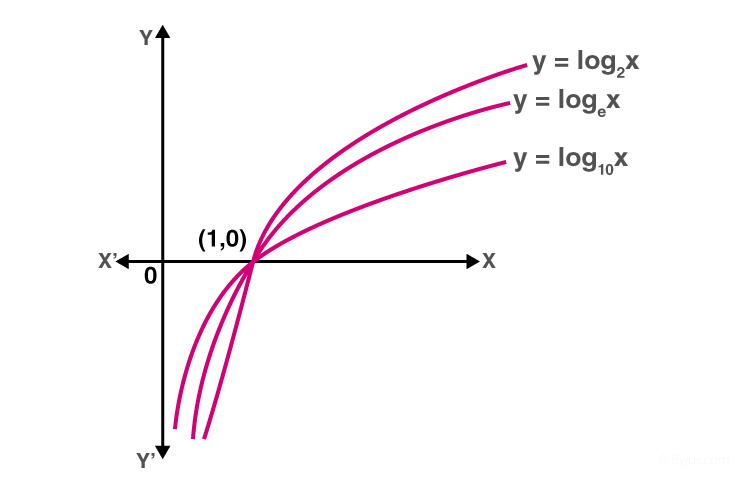
Exponential Functions Definition Formula Properties Rules

3 5 Exponential Growth Decay Ppt Download

Link Springer Com Content Pdf 10 1007 Bf Pdf

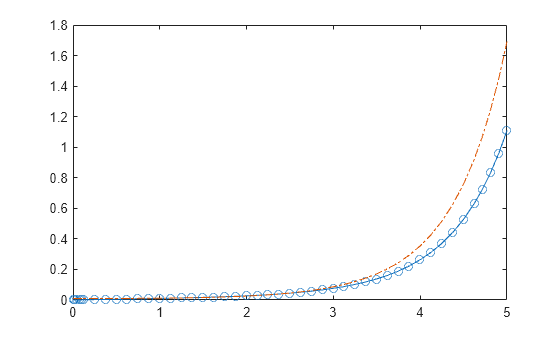
Solve Nonstiff Differential Equations Medium Order Method Matlab Ode45

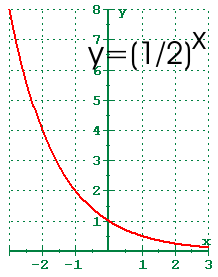
4 1 Exponential Functions And Their Graphs

Modeling Exponential Functions Ppt Download

3

Domain And Range Of Exponential And Logarithmic Functions

The Quadratic Function

Ex 1 1 1 Determine Reflexive Symmetric Transitive Ex 1 1

E Did You Hear That

Osa Fourier Based Analysis And Synthesis Of Moires In The Superposition Of Geometrically Transformed Periodic Structures

Introduction To Exponential Functions

What Is The Compound Interest Formula Robinhood

I Have Included A Few Examples And Answer Please D Chegg Com

Exponential Growth Decay Word Problems Video Khan Academy

Complex Number Wikipedia

Apps Dtic Mil Dtic Tr Fulltext U2 A Pdf

Given A Vector Space V Over The Field R An Inner Chegg Com

De Morgan S Theorem An Overview Sciencedirect Topics

Exponential Growth And Decay Youtube

Graphing Parabolas

2

When Is Y A Vowel Or Consonant Merriam Webster

Oscillation Of Second Order Nonlinear Delay Differential Equations With Nonpositive Neutral Coefficients Topic Of Research Paper In Mathematics Download Scholarly Article Pdf And Read For Free On Cyberleninka Open Science Hub

Math231 Review 2 Test Directions 1 You May Have Chegg Com

Q Tbn And9gcsvvxtcxxe7tenwsjje0nmivztankrwefyxe3qwacrrpautlw H Usqp Cau

Introduction To Exponential Functions

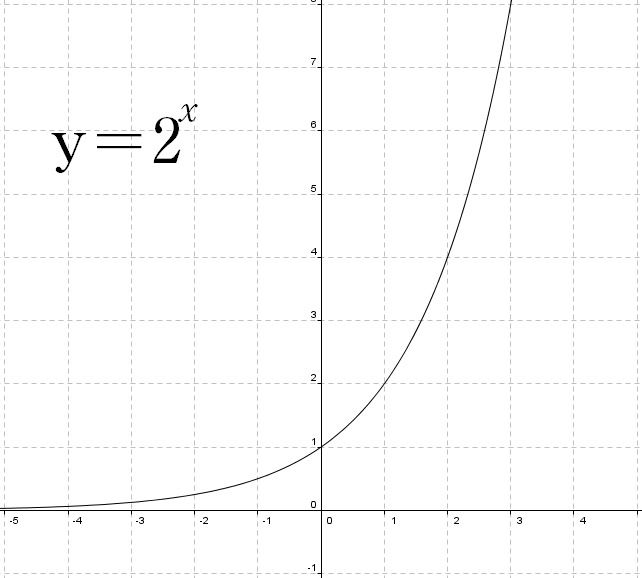
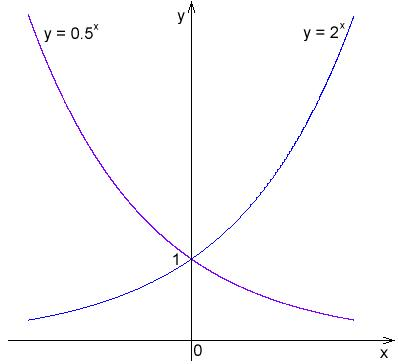
Graphs Of Exponential And Logarithmic Functions Boundless Algebra

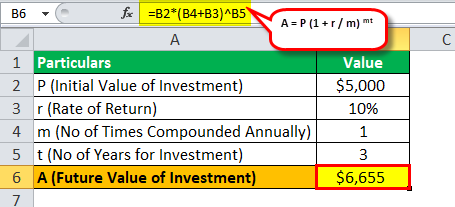
Compound Interest Examples Step By Step Examples With Formulas

Holt Algebra Exponential Growth And Decay Math Madness Round 1 Rasul Vs Soren Ppt Download

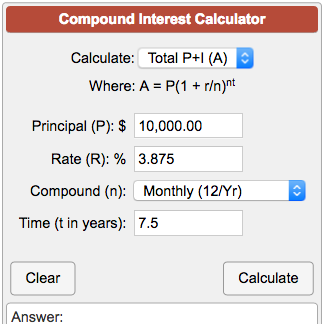
Compound Interest Calculator

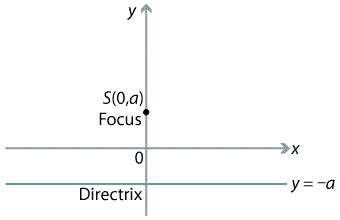
Content Focus Directrix Definition Of The Parabola

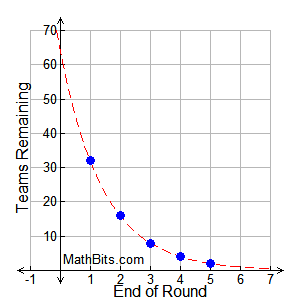
Exponential Functions Mathbitsnotebook A1 Ccss Math

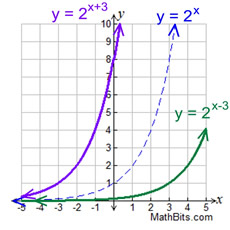
Exponential Functions Mathbitsnotebook A1 Ccss Math

The Quadratic Function

Curvature And Radius Of Curvature

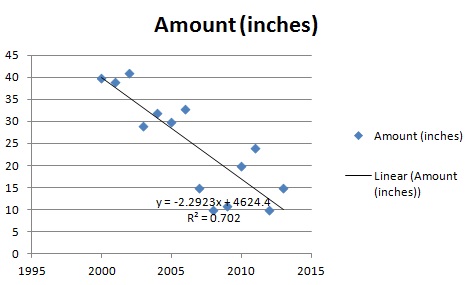
Linear Regression Simple Steps Video Find Equation Coefficient Slope Statistics How To

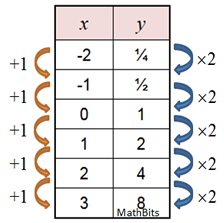
Exponential Functions Mathbitsnotebook A1 Ccss Math

Graph Y B For 0 B 1 Ppt Video Online Download

Section 1 8 Linear Differential Equations

Graphing Exponential Functions

Content Wolfram Com Uploads Sites 13 18 02 05 5 7 Pdf

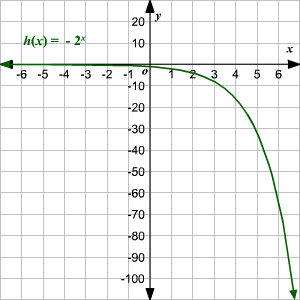
Domain And Range Of Exponential And Logarithmic Functions

Ps02 Cmth03 Unit 1

Exponential Growth And Decay Examples Solutions Videos Worksheets Activities

E Mathematical Constant Wikipedia

Exponential And Logarithmic Functions Logarithmic Functions Sparknotes

6 8 Video Lesson Exponential Growth Decay Youtube

Q Tbn And9gcr3y5vauup5hb9yslwa7xya0wuz1ghmlid5dcrczfebrxeczg Usqp Cau

Simple Examples Of Linear Maps Youtube

Curvature And Radius Of Curvature

Exponential Growth Calculator

Ex 9 3 1 Form Differential Equation X A Y B 1 Ex 9 3

What Is The Difference Between Correlation And Linear Regression Faq 1141 Graphpad

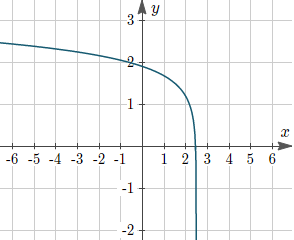
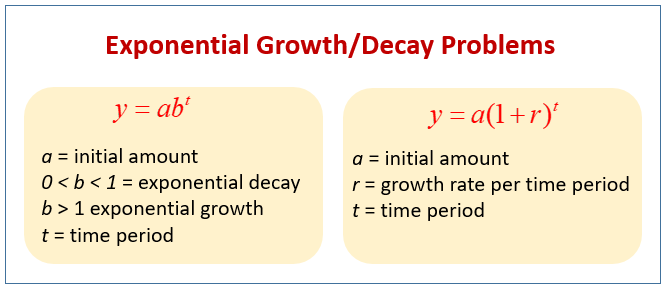
How To Find The Equation Of A Logarithm Function From Its Graph

Exponential Growth Calculator

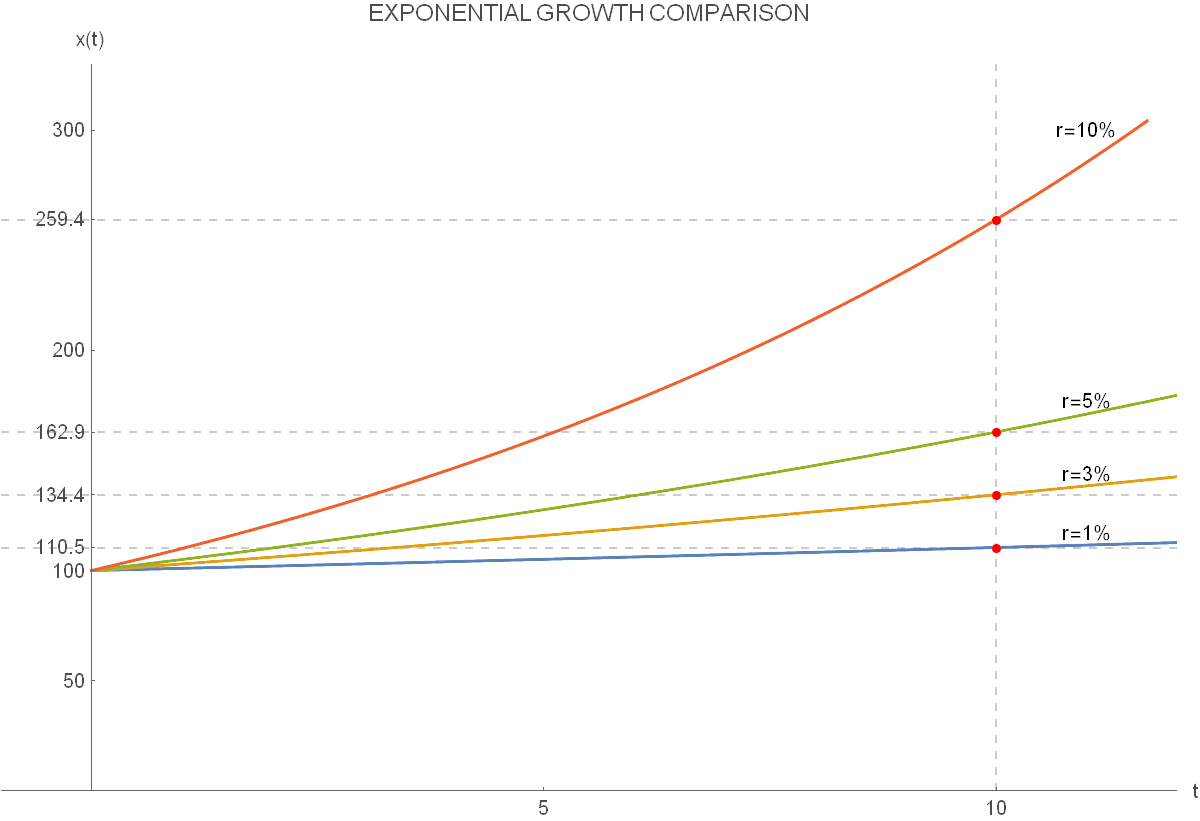
Linear Vs Exponential Functions Expii

Graphing Parabolas

2

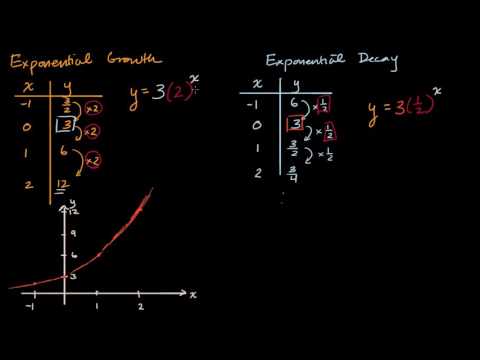
Exponential Decay Intro Video Khan Academy

Families Of Curves Differential Equation Examples Pdf Familyscopes

Incoming Term: y=a(1+r)^t examples, what is y=a(1+r)^t, y=a(1+r)^t solve for r, a=p(1+r)^t examples,